Als Nava zu Ende erzählt hatte, steckte sie sich eine Zigarette an und atmete eine lange Rauchfahne aus. Caine wusste nicht, was er sagen sollte. Ihre Geschichte klang derart an den Haaren herbeigezogen, dass er sie fast glaubte. Niemand würde eine so absurde Geschichte erzählen, wenn sie nicht stimmte. Und er fühlte sich bereits eng mit ihr verbunden, ob nun trotz oder wegen ihrer gemeinsamen Feuerprobe.
Doch dann holte ihn die Realität wieder ein. Das Spezinstitute. Terroristen. Geheimagenten. Er konnte nicht glauben, dass er die Wahrheit nicht schon früher erkannt hatte.
«O Gott», murmelte Caine. «Es ist passiert.»
«Wie bitte?»
Caine kniff die Augen zu und wollte, dass die Frau verschwand, doch als er sie wieder öffnete, saß sie immer noch neben ihm.
«Ist alles in Ordnung mit Ihnen?», fragte das Trugbild.
«Sie sind nicht real.»
«Was?»
«Sie sind nicht real. Das Ganze hier ist nicht real – es kann nicht sein. Ich habe einen schizophrenen Schub. Das ist die einzige vernünftige Erklärung hierfür.»
«David, ich versichere Ihnen …»
«NEIN!», sagte Caine mit plötzlich erhobener Stimme. «Das kann alles nicht real sein. Sie sind Teil einer Art Sinnestäuschung.»
«Wovon reden Sie?»
Caine starrte sie nur an, wusste nicht, was er tun sollte. Was hatte Jasper noch gesagt? Er legte die Stirn in Falten, blinzelte schnell und versuchte sich zu erinnern.
Gib dir Mühe, in der Welt, die du da geschaffen hast, kluge Entscheidungen zu treffen. Irgendwann findest du dann auch wieder zurück in die Realität.
Okay. Das würde er hinkriegen. Lass dich einfach treiben. Wenn er nicht zurück in die Realität konnte, würde er es einfach aussitzen. Jaspers Ratschlag hatte viel für sich; die beste Möglichkeit, verrückte Taten in der realen Welt zu vermeiden, war, sich in der Wahn-Welt so vernünftig wie möglich zu verhalten. Und wenn dies doch die Realität war – auch wenn er sich ganz sicher war, dass das nicht sein konnte –, würde er wenigstens vernünftige Entscheidungen treffen.
Durch seine pragmatische Einschätzung der Lage beruhigt, sah Caine wieder zu Nava hinüber und überlegte, was er sagen sollte. Die Antwort kam ihm sofort in den Sinn – wenn dies tatsächlich die reale Welt war, war es ganz gleich, was er sagte. Caine öffnete den Mund und hielt dann einen Moment lang inne, als ihm die Absurdität der Situation klar wurde, aber er wusste nicht, was er sonst tun sollte.
«Äh, es tut mir Leid, ich hatte nur … kurz das Gefühl, nicht mehr ich selbst zu sein.»
«Ist alles in Ordnung mit Ihnen?», fragte das Trugbild – Nava, sie sagte, ihr Name sei Nava.
«Ja, mir geht’s gut», sagte Caine. Er fühlte sich immer noch seltsam, bekam seinen neuen mentalen Zustand aber schnell in den Griff. Er versuchte nun, zu geistiger Klarheit zurückzufinden. «Das war wirklich eine unglaubliche Geschichte, aber sie erklärt nicht, woher Sie meinen Namen kennen. Und warum Sie mich gerettet haben.»
Nava guckte bedrückt. «Da war … eine Frau. Sie hat mir von Ihnen erzählt – wer Sie sind, wo Sie sein würden, alles. Und die genaue Zeit Ihres Todes, wenn ich nicht da wäre, um Sie zu retten.»
Ihre Antwort war eher verwirrend als erhellend. «Das erklärt noch nicht, woher diese Frau von mir wusste. Oder warum Sie beschlossen, mich zu retten.»
«Um ehrlich zu sein», sagte Nava, «war mein ursprünglicher Plan nicht, Sie zu retten, sondern Sie zu kidnappen.»
«Um mich der RDEI zu übergeben?», fragte Caine.
«Genau.»
«Und warum haben Sie es sich anders überlegt?»
«Wegen dieser Frau. Sie kannte … sie kannte meinen Namen. Meinen wirklichen Namen. Und sie wusste von … sie wusste Dinge, die sie unmöglich wissen konnte. Es sei denn, die Theorie des Professors stimmt.»
Caine begann zu frösteln. «Welcher Professor? Welche Theorie?»
«Der Professor, der vor zwei Tagen die Tests an Ihnen durchgeführt hat.»
Caine spürte, wie sein Herz erstarrte. Nava nickte. «Die NSA hat ihn überwacht. Sie haben Daten in die Hände bekommen, aus denen hervorgeht, dass er in letzter Zeit Fortschritte beim Erreichen … seines Ziels gemacht hat.»
«Und was war sein Ziel?», fragte Caine, obwohl ein Teil von ihm die Antwort bereits kannte.
«Er war überzeugt, dass er eine Möglichkeit gefunden hatte, die Zukunft vorherzusagen.»
Caine wurde schlecht. Das Trugbild erschien allmählich allzu real. Erneut kamen ihm Jaspers Worte in den Sinn.
Man spürt gar nichts davon … Das ist ja gerade das Unheimliche daran.
Sein Bruder hatte Recht gehabt, denn Caine war in seinem Leben noch nie so unheimlich zumute gewesen. Er hatte plötzlich großen Respekt vor seinem Zwillingsbruder.
«Alles in Ordnung mit Ihnen?», fragte Nava.
Caine ignorierte die Frage und stellte stattdessen selbst eine. «Diese Theorie … hat sie einen Namen?»
«Ja», sagte Nava. «Der Laplace’sche Dämon. Sagt Ihnen das etwas?»
Caine nickte, doch er war mit seinen Gedanken woanders und versuchte, die Einzelteile zusammenzusetzen.
«Ich habe alle seine Abstracts im STR-Labor überflogen», sagte Nava. «Die meisten hatten mit Physik, Biologie und Statistik zu tun, aber am Ende gab es einen ganzen Abschnitt über den Laplace’schen Dämon. Ich hatte keine Zeit, ihn gründlich zu lesen, aber anscheinend sprach er über das Okkulte.»
«Nicht über das Okkulte», sagte Caine. «Über Wahrscheinlichkeitstheorie.»
Nava sah ihn verständnislos an. «Ich kann Ihnen nicht folgen.»
Caine seufzte, wusste nicht recht, wo er beginnen sollte oder ob es überhaupt notwendig war, dies alles einer Halluzination zu erklären, die lediglich ein Produkt seines eigenen Unterbewusstseins war. Aber vielleicht war es genau das, was er wollte: eine Erklärung. Caine sah an Nava vorbei und suchte nach der besten Möglichkeit, es zu erklären. Er hatte Laplaces Werke zwar jahrelang studiert, wusste aber nicht, wo er anfangen sollte, und deshalb erzählte er einfach drauflos.
«Im ausgehenden siebzehnten und frühen achtzehnten Jahrhundert lebte in London ein französischer Statistiker namens Abraham de Moivre. Während die Statistik noch in den Kinderschuhen steckte, konnte Moivre seinen Unterhalt damit verdienen, Gewinnchancen für die Spieler der Stadt zu berechnen.
Das machte er ungefähr zehn Jahre lang, dann schrieb er ein Buch mit dem Titel Die Lehre des Zufalls. Obwohl es nur 52 Seiten lang war, war es einer der wichtigsten Texte zur Mathematik seiner Zeit, denn es bildete die Grundlage der Wahrscheinlichkeitsrechnung, die er anhand von Problemen beim Würfeln oder anderen Spielen erklärte.
Die Sache ist allerdings die, dass de Moivre, anders als der Titel des Buches suggeriert, nicht an den Zufall glaubte.»
«Wie meinen Sie das?», fragte Nava.
«De Moivre glaubte, dass der Zufall eine Illusion sei. Er stellte die These auf, dass niemals etwas ‹zufällig› geschieht – dass jedes scheinbar zufällige Ereignis auf eine Ursache zurückgeführt werden kann.» Nava guckte verwirrt, deshalb griff Caine zu seinem erprobten Notanker der Wahrscheinlichkeitsrechnung: Im Zweifelsfall spricht man am besten über Münzen.
«Okay», sagte er, langte vorsichtig und aufstöhnend in seine Hosentasche und holte einen Vierteldollar hervor. «Wenn ich diese Münze werfe, dann würden Sie sagen, es ist reines Glück oder Zufall, ob Kopf oder Zahl oben landet, richtig?»
«Tja, da liegen Sie falsch. Wenn man in der Lage wäre, alle physikalischen Faktoren zu bestimmen, die den Wurf der Münze beeinflussen – den Winkel meiner Hand, die Entfernung zum Boden, die Kraft, mit der ich die Münze in die Luft werfe, den Windzug, die Zusammensetzung der Münze et cetera, et cetera –, dann wäre man in der Lage, mit hundertprozentiger Genauigkeit das Ergebnis des Wurfes vorherzusagen, denn die Münze unterliegt den Gesetzen der Newton’schen Physik, die absolute Gültigkeit haben.»
Nava zündete sich eine Zigarette an und ließ sich seine Worte durch den Kopf gehen. «Ich kenne mich damit nicht aus, David, aber ist es nicht unmöglich, all diese Faktoren genau zu berechnen?»
«Für Menschen? Ja, stimmt», sagte Caine. «Aber dass wir diese Faktoren nicht berechnen können, bedeutet nicht, dass das Ergebnis des Münzwurfs dem Zufall unterliegt. Es bedeutet lediglich, dass wir, als menschliche Wesen, nicht die Fähigkeit besitzen, alle Facetten des Universums zu berechnen. Daher mögen Ereignisse zufällig erscheinen, obwohl sie gänzlich bestimmt sind durch physikalische Gegebenheiten.
Diese Denkrichtung nennt man Determinismus. Deterministen glauben, dass nichts unbestimmt ist, dass alle Geschehnisse eine Wirkung früherer Ursachen sind, selbst wenn wir die Ursachen nicht kennen.»
«Wenn ich auf einer belebten Straße einem Freund begene, ist das also kein Zufall?», fragte Nava.
«Nein», antwortete Caine. «Überlegen Sie mal. Man geht doch nie zufällig irgendwohin, oder? Das Ziel hängt immer von körperlichen, emotionalen und geistigen Ursachen ab. Und das trifft auf jeden anderen Menschen ebenfalls zu. Das ‹willkürliche› Treffen auf einen Freund mag wie ein Zufall erscheinen, es ist aber keiner.
Stellen Sie sich einen Computer vor, der sowohl in Ihr Gehirn und in Ihre Muskeln schauen kann als auch in die Ihres Freundes. Wenn der Computer zudem alle äußeren Bedingungen der Minuten oder Stunden, die zu Ihrem Treffen führen, kennen würde, dann könnte er voraussagen, wann, wo und wie Sie sich treffen werden. Daher ist das berühmte ‹Sich-zufällig-über-den-Weg-Laufen› alles andere als ein Zufall – es ist vorhersagbar.»
«Aber in der wirklichen Welt», sagte Nava langsam, «ist es nicht vorhersehbar, wann man sich ‹zufällig› über den Weg läuft.»
Caine schüttelte den Kopf. «Nein, ist es nicht. Da es einen Computer, wie ich ihn eben beschrieben habe, nicht gibt, können wir ein solches Ereignis nicht vorhersagen. Das bedeutet aber noch lange nicht, dass das Ereignis an sich unvorhersagbar ist. Es bedeutet nur, dass wir es nicht vorhersagen können. Verstehen Sie den Unterschied?»
Nava nickte langsam, als sie begriff.
«Das ist eine schöne Theorie», sagte sie, «aber in der wirklichen Welt funktioniert sie nicht.»
«Tja, de Moivre sah das anders. Er bediente sich ständig der Mathematik und Physik, um scheinbar unvorhersagbare Phänomene vorherzusagen, sogar sein eigenes Todesdatum.»
«Wie hat er das gemacht?», fragte Nava.
«In den letzten Monaten seines Lebens fiel de Moivre auf, dass er jede Nacht fünfzehn Minuten länger schlief. Als Determinist schloss er aus diesem Wissen, dass er, wenn der Schlaf weiterhin im gleichen Maße zunahm, in der Nacht, in der er ‹planmäßig› vierundzwanzig Stunden durchschliefe, sterben würde. Er sagte voraus, dass dies am 27. November 1754 eintreten würde. Und als dieser Tag kam, starb de Moivre, genau wie vorhergesagt.»
«Das beweist kaum seine Theorie», erwiderte Nava skeptisch.
«Nein, stimmt. Aber Sie müssen zugeben, dass es schon interessant ist, dass es da einen Mann gab, der davon überzeugt war, alles sei vorhersehbar, wenn man nur die richtigen Berechnungen anstelle, und dem es dann gelang, seinen eigenen Todestag zu berechnen», sagte Caine, mit einem Mal traurig. Die beiden schwiegen eine Weile, dann fuhr Caine fort.
«Jedenfalls diente de Moivres Lehre des Zufalls als Grundlage für das Werk eines anderen, sehr berühmten französischen Mathematikers namens Pierre Simon de Laplace.»
Als Caine den Namen aussprach, erinnerte er sich plötzlich an den stickigen, holzvertäfelten Raum in der Columbia University, in dem er einmal Seminare gegeben hatte. Obwohl es über ein Jahr her war, dass er Vorlesungen über diesen Statistiker aus dem achtzehnten Jahrhundert gehalten hatte, konnte er sich noch gut an den Unterricht erinnern.
«Wie die meisten von uns in diesem Raum wurde Laplace von seinen Eltern nicht verstanden», sagte Caine und ging dabei vor der Tafel auf und ab.
«Sein Vater wollte, dass er Soldat oder Priester wurde, aber Laplace entschied sich für eine akademische Laufbahn. Daher ging er mit achtzehn Jahren nach Paris, dem geistigen Zentrum Frankreichs. Dort unterrichtete er die Kadetten einer Militärschule in Geometrie. Unter ihnen befand sich auch ein kleiner Junge namens Napoleon Bonaparte, der später, glaube ich, einige ziemlich sonderbare Dinge angestellt hat.»
Das brachte Caine von den zwölf Studenten, die sich um den Tisch drängten, ein Kichern ein.
«1770 präsentierte Laplace seine erste Arbeit der renommierten Pariser Académie des Sciences. Danach war jedem klar, dass er ein mathematisches Genie war. Und so widmete er den Rest seines Lebens zwei Gebieten: der Wahrscheinlichkeitsrechnung und der Astronomie. Fast dreißig Jahre später, 1799, verschmolz er beide Gebiete, als er das wichtigste Werk zur Astronomie jener Zeit veröffentlichte: Méchanique Céleste oder Himmelsmechanik. Das Buch beinhaltete nicht nur eine Erörterung des Sonnensystems, es enthielt auch neue Methoden zur Berechnung der Umlaufbahn von Planeten.
Dass Méchanique Céleste noch heute als wichtig erachtet wird, liegt jedoch nicht an Laplaces astronomischen Erkenntnissen, sondern daran, dass er der erste Wissenschaftler war, der die Wahrscheinlichkeitsrechnung auf die Astronomie anwandte. Er zeigte, dass wiederholte Beobachtungen der Position eines Sterns dazu tendierten, die Glockenkurve zu bestätigen, welche de Moivre in der Lehre des Zufalls beschrieben hatte. Mit Hilfe der Wahrscheinlichkeitsrechnung war Laplace letztlich dazu in der Lage, die Position der Planeten vorauszusagen und das Universum besser zu verstehen.»
«Was meinen Sie mit ‹wiederholte Beobachtungen der Position eines Sterns›?», fragte ein blasser Student mit dunklem, langem Haar.
«Gute Frage», entgegnete Caine und ging an die Tafel. «Eines der größten Probleme der Astronomie war damals, dass jeder seine Messungen per Hand vornahm. Und da Menschen Fehler machen, waren die Daten ungenau. Wenn zwanzig verschiedene Astronomen die Position eines Sterns maßen, erhielt man zwanzig verschiedene Ergebnisse.
Laplace nahm jedenfalls diese zwanzig verschiedenen Beobachtungen und stellte sie graphisch dar. Dabei sah er, dass die Positionen auf einer Glockenkurve wie dieser lagen.» Caine zeigte auf das Schaubild einer Normalverteilung an der Wand.
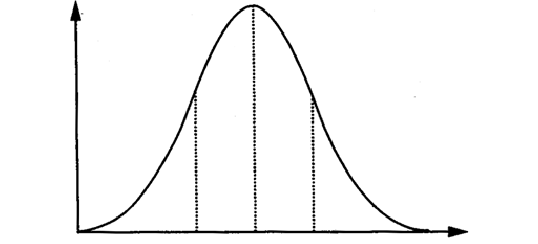
«Als er das sah, sagte er sich: ‹Aha, wenn die Beobachtungen einer Normalverteilung entsprechen und die Spitze der Glockenkurve den wahrscheinlich wahren Wert der Stichprobe zeigt, dann ist die Spitze wahrscheinlich die wahre Position des Sterns.› Heute erscheint uns das offensichtlich, aber damals war es revolutionär. Es war das erste Mal, dass jemand die Wahrscheinlichkeitsrechnung auf eine andere Disziplin anwandte. Laplace stellte die These auf, dass, selbst wenn es unmöglich sei, die genaue Position eines Sterns zu kennen, es aber dennoch möglich sei, sie mit einem bestimmten Grad der Wahrscheinlichkeit zu kennen.»
Caine hielt inne, um sicherzugehen, dass ihm alle folgen konnten.
«Doch damit endeten Laplaces Studien nicht. 1805 veröffentlichte er den vierten Band der Méchanique Céleste, in dem er mit einem neuen, philosophischen Ansatz an die Physik heranging. Er stellte die Theorie auf, dass jedes Naturphänomen durch das Studium der Kräfte zwischen Molekülen verstanden werden könne. Anhand dieser neuen Theorie untersuchte er alles Mögliche, vom Luftdruck bis zur astronomischen Brechung, wobei er erneut Handwerkszeug der Wahrscheinlichkeitsrechnung wie Glockenkurven benutzte, um die unterschiedlichsten Phänomene zu messen.
Laplaces Glanzleistung war die Veröffentlichung der Théorie Analytique des Probabilités oder Analytische Theorie der Wahrscheinlichkeiten im Jahr 1812. In diesem Werk entwickelte er die Methode der Abweichung und die Bedeutung der Fehlerminimierung …»
Ein pummeliger Student namens Steve meldete sich. «Da komme ich nicht mehr mit.»
Caine erinnerte sich daran, dass seine Vorlesung auch eine Pflichtveranstaltung für das Geschichtsstudium war und daher keine statistischen Vorkenntnisse vorausgesetzt wurden. Da in der Vorlesung noch drei weitere Studenten mit Hauptfach Geschichte saßen, musste er erklären, was er mit Fehlerminimierung meinte. Er kratzte sich am Kopf und überlegte, wo er beginnen sollte.
«Kennen Sie den Unterschied zwischen Statistik und Wahrscheinlichkeit?»
Steve und die anderen Nichtmathematiker schüttelten den Kopf.
«Okay. Die Wahrscheinlichkeitsrechnung befasst sich mit so genannten ‹zufälligen› Ereignissen wie dem Würfeln oder dem Werfen einer Münze; die Statistik bezieht sich auf die Erfassung und Auswertung von ‹tatsächlichen› Ereignissen wie Geburtenraten oder Sterblichkeitsziffern. Mit anderen Worten: Die Wahrscheinlichkeitsrechnung wird angewandt, um Gleichungen aufzustellen, die Statistiken vorhersagen.»
Da Caine zwar das Gefühl hatte, dass Steve ein Licht aufgegangen war, er jedoch nicht wusste, wie es um die beiden anderen bestellt war, griff er auf seinen Notanker zurück.
«Beginnen wir mit einem einfachen Beispiel. Nehmen wir an, ich werfe viermal hintereinander eine Münze. Wie oft werde ich Ihrer Meinung nach einen Kopf werfen?»
«Zweimal», sagte Steve.
«Und warum?»
«Weil man bei der Hälfte der Würfe einen Kopf wirft, und die Hälfte von vier ist zwei.»
Caine nickte. «Im Grunde haben Sie gerade die Wahrscheinlichkeitsrechnung angewandt, um eine Statistik vorherzusagen – die Anzahl der Köpfe. Bewusst oder unbewusst haben Sie eine Gleichung aufgestellt, um das Problem zu lösen.» Caine schrieb an die Tafel:

«Wir wissen nun zwar, dass bei vier Münzwürfen höchstwahrscheinlich zwei Köpfe und zwei Zahlen herauskommen werden, aber glauben Sie auch, dass jedes Mal exakt zwei Köpfe geworfen werden?»
«Nein.»
«Korrekt. Denn tatsächlich werden meistens nicht zwei Köpfe geworfen.»
Steve guckte verwirrt. «Moment mal, sagten Sie nicht gerade, dass höchstwahrscheinlich zwei Köpfe geworfen werden?»
«Das ist richtig.»
«Dann verstehe ich das nicht. Kommen nicht wenigstens jedes zweite Mal zwei Köpfe dabei heraus?»
«Nein. Es gibt sechzehn mögliche Ergebnisse, wenn man eine Münze viermal hintereinander wirft. Ich zeige es Ihnen.»

«Verstehen Sie? Von den sechzehn verschiedenen Möglichkeiten resultieren nur sechs in zwei Köpfen und zwei Zahlen. Daher werden bei zehn von sechzehn Versuchen oder in 62,5 Prozent der Fälle nicht zwei Köpfe geworfen. Deshalb frage ich Sie noch einmal: Wenn ich Ihnen sage, dass ich eine Münze viermal hintereinander werfen werde, wie viele Köpfe erhalte ich dann Ihrer Meinung nach?»
Steve starrte die Gleichung an, die Caine an die Tafel geschrieben hatte, und zog nachdenklich die Stirn in Falten. «Ich würde immer noch zwei sagen.»
«Warum würden Sie zwei sagen, nachdem ich Ihnen gerade gezeigt habe, dass Sie damit in 62,5 Prozent der Fälle falsch liegen werden?», fragte Caine.
«Weil ich bei jeder anderen Anzahl in noch mehr als 62,5 Prozent der Fälle falsch liegen würde.»
«Ganz genau», sagte Caine und schnippte mit den Fingern. «Hätten Sie einen Kopf oder drei Köpfe gesagt, würden Sie in 75 Prozent der Fälle falsch liegen, und hätten Sie keinen Kopf oder vier Köpfe gesagt, würden Sie in 93,75 Prozent der Fälle falsch liegen.» Caine lächelte. «Indem Sie zwei Köpfe gesagt haben, haben Sie die Antwort gewählt, welche die Wahrscheinlichkeit, falsch zu liegen, minimiert. Das ist die Grundlage der gesamten Wahrscheinlichkeitsrechnung: die Minimierung von Fehlern.
Obwohl das Ergebnis bei den Würfen wahrscheinlich ein anderes ist als zwei Köpfe, ist Ihre ursprüngliche Gleichung
K = 0,5 x W
immer noch gültig, denn sie beschreibt das Phänomen am besten. Eine andere Möglichkeit, dies zu überprüfen, ist, die Daten graphisch darzustellen. Wie Sie sehen können, handelt es sich um eine Glockenkurve, und die Spitze der Kurve spiegelt die natürliche Tendenz des Phänomens wider.
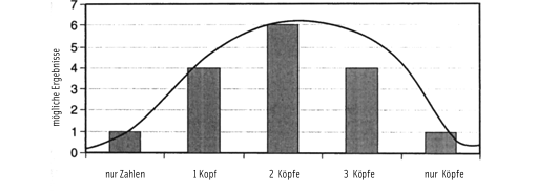
Laplace hat ungefähr das Gleiche getan, nur dass er nicht die Anzahl der Köpfe beim Münzwurf vorhergesagt hat, sondern Tausende von astronomischen Beobachtungen benutzt und Gleichungen entwickelt hat, um die Umlaufbahnen von Planeten vorherzusagen.»
«Okay, ich hab’s kapiert», sagte Steve. «Aber ich verstehe immer noch nicht, warum es wichtig ist.»
«Es ist wichtig, weil es demonstriert, wie die Wahrscheinlichkeitsrechnung funktioniert. Laplace zeigte, dass die beste Möglichkeit, die Realität vorherzusagen, nicht darin besteht, die richtige Antwort zu errechnen, sondern darin, die Antwort zu finden, die am wenigsten falsch ist. Obwohl die Wahrscheinlichkeit in dem Münzbeispiel, bei vier Würfen zwei Köpfe zu erhalten, nur bei 37,5 Prozent liegt, ist es noch unwahrscheinlicher, jede andere Anzahl von Köpfen zu erhalten. Ihre Vorhersage, zwei Köpfe zu erhalten, ist daher diejenige, die am wenigsten falsch ist, und deshalb die richtigste.
Aus diesem Grund konnte Laplace die Umlaufbahn der Planeten vorhersagen, während andere es nicht konnten. Er entwickelte Gleichungen, welche die Abweichungen der Daten aller Astronomen minimierten, und war deshalb in der Lage, Umlaufbahnen von Planeten festzulegen, welche die geringste Wahrscheinlichkeit aufwiesen, falsch zu sein.»
«Und so die höchste Wahrscheinlichkeit, richtig zu sein», sagte Steve.
«Genau», sagte Caine, erfreut, dass Steve anscheinend verstanden hatte. «Wichtig ist festzuhalten, dass man sich durch diese Methode, genauso wie durch alle anderen Methoden der Wahrscheinlichkeitsrechnung, niemals einer Sache absolut sicher sein kann, da das Ziel der vorhersagenden Gleichungen die Minimierung von Fehlern ist, und nicht ihre Eliminierung.»
«Warum würde man Fehler nicht eliminieren wollen?», fragte ein dunkelhaariges Mädchen namens Colleen.
«Das will man schon. Doch es ist unmöglich, Fehler völlig zu eliminieren, da man nie genügend Informationen besitzt, um eine Gleichung aufzustellen, die alles perfekt vorhersagt.»
«Warum nicht?»
«Denken Sie an Umfragen, die Sie vor einer Wahl in der Zeitung lesen. Sie sind nie hundertprozentig korrekt, weil es schlicht unmöglich ist, jeden Wähler zu befragen. Indem man jedoch eine kleine Auswahl von Leuten aus verschiedenen sozioökonomischen Schichten befragt, sind die Meinungsforscher in der Lage, Gleichungen aufzustellen, die mit einer gewissen Wahrscheinlichkeit vorhersagen, wer die Wahl gewinnen wird. Deshalb sind solche Umfragen nur mit einer Toleranz von ein oder zwei Prozent richtig. Denn Umfrageergebnisse sind immer Wahrscheinlichkeiten und nie Gewissheiten.
Die Wahrscheinlichkeitsrechnung gibt Wissenschaftlern also die Freiheit, eine Antwort als richtig anzunehmen, obwohl sie sich nicht hundertprozentig sicher sind. Sie zeigt, dass man bei minimaler Möglichkeit, falsch zu liegen, wahrscheinlich die Wahrheit entdeckt hat.»
Caine schwieg einen Moment lang, um das Gesagte bei seinen Zuhörern sacken zu lassen, dann fuhr er fort.
«Und das führt uns zu Laplaces umstrittenster Theorie, die häufig sein ‹Dämon› genannt wird. Zwei Jahre nachdem er Théorie Analytique des Probabilités veröffentlicht hatte, schrieb er den Essai Philosophique sur les Probabilités oder den Philosophischen Versuch über die Wahrscheinlichkeit. Darin befand sich sein zweitberühmtestes Zitat.» Caine sah in seine Notizen und las das Zitat laut vor.
Eine Intelligenz, die für einen gegebenen Augenblick alle in der Natur wirkenden Kräfte, sowie die gegenseitige Lage der sie zusammensetzenden Elemente kennte, und überdies umfassend genug wäre, um die gegebenen Größen der Analysis zu unterwerfen, werde in derselben Formel die Bewegungen der größten Weltkörper wie des leichtesten Atoms umschließen; nichts wäre für sie ungewiss und Zukunft und Vergangenheit würden ihr offen vor Augen liegen.
«Da er Determinist war», fuhr Caine fort, «nahm Laplace an, dass jemand, der alle Gesetze der Physik versteht und zu jedem Zeitpunkt die Position jedes subatomaren Teilchens im Universum kennt, alles wissen würde, was jemals passiert ist, und mit absoluter Genauigkeit die gesamte zukünftige Geschichte vorhersagen könnte.»
«Aber es ist unmöglich, alles zu wissen», sagte Colleen.
«Nichts ist unmöglich», entgegnete Caine, «auch wenn bestimmte Dinge sehr unwahrscheinlich sind.» Er trank einen Schluck Cola, während die Studenten seine Worte überdachten. «Wissenschaftler bezeichnen seine Theorie heute als den Laplace’schen Dämon.»
«Warum wird sie sein Dämon genannt?», fragte Steve. «Hat die Theorie ihn gequält?»
«Nein, das ist ein geläufiges Missverständnis» antwortete Caine. «Sie hat ihn überhaupt nicht gequält, denn Laplace war davon überzeugt, dass er Recht hatte. Nach seinem Tod übernahmen Wissenschaftler den Begriff ‹Laplace’scher Dämon›, um eine allwissende Intelligenz zu beschreiben. Ein Wesen, das die Fähigkeit besitzt, alles Gegenwärtige zu wissen, und deshalb auch alles Vergangene und Zukünftige weiß.»
«Klingt wie ein Gott», sagte Colleen.
«Ja», erwiderte Caine nachdenklich. «So was in der Art.»
Nava baute ihm eine Schiene, während Caine zum Ende seiner Vorlesung kam. Anschließend schwieg Nava sehr lange, ehe sie die Stille wieder durchbrach.
«David», sagte sie, «die Wissenschaftler der STR glauben, dass Sie der Laplace’sche Dämon sind.»
Caine schüttelte den Kopf. «Das ist verrückt. Der Laplace’sche Dämon existiert nicht, er ist ein theoretisches Konstrukt. Er ist nur ein Konzept, das eine allwissende Intelligenz beschreibt, die die Zukunft vorhersagen kann.»
Er hielt inne. Ihm schwirrte der Kopf. «Außerdem wurde Anfang des zwanzigsten Jahrhunderts bewiesen, dass der Laplace’sche Dämon unmöglich ist.»
«Wie das?», fragte Nava.
«Ein Physiker namens Werner Heisenberg wies nach, dass subatomare Teilchen keine bestimmte Position haben, ehe sie beobachtet werden.»
Nava hob die Augenbrauen, worauf Caine sofort reagierte. «Fragen Sie nicht – das ist Quantenphysik, das soll keinen Sinn ergeben.»
«Okay, schön. Aber warum wird dadurch der Laplace’sche Dämon unmöglich?»
«Wenn subatomare Teilchen zur gleichen Zeit verschiedene Positionen einnehmen, ist es für jede Intelligenz unmöglich – selbst für eine allwissende –, die genaue Position eines jeden Teilchens zu kennen, eben weil sie keine exakten Positionen haben. Und da dieses Wissen zur Vorhersage der Zukunft erforderlich ist, kann man die Zukunft unmöglich vorhersagen. Daher ist auch der Laplace’sche Dämon ein Ding der Unmöglichkeit.
Außerdem», fügte Caine hinzu, «weiß ich weder alles, noch kann ich die Zukunft vorhersagen.»
«Und was war in dem Restaurant?», entgegnete Nava.
Caine spürte, wie ihm kalt wurde. «Woher wissen Sie davon?»
«Die NSA hat es beobachtet.» Nava beugte sich vor. «Ich habe gesehen, was passiert ist, David. Ich habe gesehen, wie Sie eine Sekunde, bevor der Pickup durch die Wand geflogen kam, jeden aus der Gefahrenzone gezogen haben. Wenn das keine Vorhersage der Zukunft war, was war es dann?»
«Hören Sie, ich habe keine Ahnung, was in diesem Restaurant geschehen ist. Nennen Sie es Intuition, zum Teufel, meinetwegen auch Vorahnung. Aber das macht mich nicht zu einer allwissenden Intelligenz.» Caine fuhr sich mit der Hand durch sein zerzaustes Haar. «Mein Gott, wenn ich alles wüsste, glauben Sie, dass ich der Russenmafia dann zwölftausend Dollar schulden würde? Nava, ich kann nicht einmal die nächste Karte vorhersagen, geschweige denn die gesamte Zukunft.»
Doch schon als Caine seine Worte hörte, wurde ihm klar, dass sie nicht ganz der Wahrheit entsprachen. Hatte er nicht gewusst, dass die Explosion ihn töten würde, wenn er keinen Ausweg fand? Hatte er nicht den Koffer geworfen, der die Kettenreaktion auslöste, die es Nava ermöglichte, rechtzeitig zu ihm zu gelangen? Caine kamen nur noch Dinge in den Sinn, die schier unmöglich waren.
Plötzlich wurde ihm noch klarer, dass das Ganze eine Wahnvorstellung war. Vielleicht funktionierte seine Geistesübung – vielleicht war er kurz davor, einen Weg zurück zur geistigen Klarheit zu finden. Er fühlte sich bereits konzentrierter, aufmerksamer. Er beschloss weiterzumachen.
«Okay, sagen wir mal, ich bin …», Caine hielt inne, «… was Sie sagen. Was machen wir jetzt?»
«Egal, ob Sie der Laplace’sche Dämon sind oder nicht, wir müssen hier weg.» Nava deutete auf einen Streifen Sonnenlicht auf dem Boden. «Es ist fast neun. Wenn wir zu lange hier bleiben, werden sie uns finden.»
«Wer sind ‹sie› eigentlich genau?», fragte Caine.
«FBI, NSA, RDEI – suchen Sie es sich aus», antwortete Nava ernst.
Er nickte. Es spielte sowieso keine Rolle. Es war alles ein Traum. Er konnte genauso gut Navas Instinkt folgen und abhauen. Sie kniete sich neben ihn und legte sich seinen Arm über die Schulter.
«Stützen Sie sich auf mich und versuchen Sie aufzustehen.» Caine tat, was sie verlangte, und versuchte mit seinem rechten Bein zu helfen, als sie ihn in einer flüssigen Bewegung vom Boden hob. Sie war noch kräftiger, als sie aussah. Er belastete seinen linken Fuß ein wenig, doch sofort wurde ihm schwindelig und schwarz vor Augen.
«Hey!» Nava packte ihn mit dem anderen Arm und hielt ihn eng an ihrem Körper. Er kam wieder zu sich.
«Was war los?», fragte Caine.
«Sie wären fast ohnmächtig geworden», sagte sie. «Meinen Sie, Sie können stehen, wenn ich jetzt loslasse?»
Caine verlagerte sein Gewicht erneut vorsichtig auf den linken Fuß und nickte. Langsam ließ sie ihn los und trat einen Schritt zurück. Caine schwankte ein wenig, blieb aber auf den Beinen. Ein weiterer Schwindelanfall überkam ihn, doch er schloss die Augen und ließ ihn vorbeigehen, während er sich auf dem Kühlschrank abstützte.
«Glauben Sie, Sie werden nochmal ohnmächtig?»
«Ich glaube nicht.» Er hüpfte vorsichtig ein paar Schritte vorwärts. «Aber ich glaube, ich wäre schneller mit einer Krücke oder so.»
Sie nickte. «Stimmt. Ich bin gleich wieder da.» Sie öffnete die Tür und verließ die Wohnung. Er hörte ein Geräusch, als würde Brennholz gehackt.
«Hier, versuchen Sie es damit», sagte sie, als sie mit einem behelfsmäßigen Gehstock wiederkam. Er nahm ihn vorsichtig und achtete darauf, nicht die scharfen Kanten zu berühren.
«Ja», sagte er, «das wird gehen.»