During the writing of this book there were four tomes that were always on my desk, and whose contribution cannot be isolated to any individual chapter. Martin Gardner remains peerless in popular maths for his erudition, wit and clarity. Tobias Dantzig’s Number is a classic about the cultural evolution of mathematics. Both the Ifrah and the Cajori are painstakingly well researched and endlessly fascinating.

 

Cajori, F., A History of Mathematical Notations, Dover, 1993 (facsimile of original by Open Court, Illinois, 1928/9)

Dantzig, T., Number, Plume, New York, 2007 (originally Macmillan, 1930)

Gardner, M., Mathematical Games: The Entire Collection of His Scientific American Columns, Mathematical Association of America, 2005

Ifrah, G., The Universal History of Numbers, John Wiley, New York, 2000

CHAPTER ZERO

This chapter is based on conversations in London with Brian Butterworth, and in Paris with Stanislas Dehaene and Pierre Pica. At University College London I was screened for dyscalculia by Teresa Iuculano and Marinella Cappelletti, with a computer program now used in schools in the UK. I’m not dyscalculic, which is probably no great surprise. If you would like to help support the Munduruku’s protection of their traditional education and environment, donations can be sent to: The Munduruku Fund, The Arrow Rainforest Foundation, 5 Southridge Place, London SW20 8JQ, United Kingdom. More details can be found on: www.thearrowrainforestfoundation.com

 

Butterworth, B., The Mathematical Brain, Macmillan, London, 1999

Dehaene, S., The Number Sense, Oxford University Press, Oxford, 1997

Matzusawa, T. (ed.), Primate Origins of Human Cognition and Behavior, Springer, Tokyo, 2001

 

Angier, N., ‘Gut Instinct’s Surprising Role in Math’, New York Times, 2008

Dehaene, S., Izard, V., Spelke, E., and Pica, P., ‘Log or Linear?’, Science, 2008

Inoue, S., and Matsuzawa, T., ‘Working memory of numerals in chimpanzees’, Current Biology, 2007

Pica, P., Lerner, C., Izard, V., and Dehaene, S., ‘Exact and Appropriate Arithmetic in an Amazonian Indigene Group’, Science, 2004

Siegler, R.S., and Booth, J.L., ‘Development of Numerical Estimation in Young Children’, Child Development, 2004

CHAPTER ONE

Anyone wanting more information about the joys of base 12 can reach the Dozenal Society of America at [email protected], or 5106 Hampton Avenue Suite 205, Saint Louis, Missouri 63109-3115, USA. Little Twelvetoes is a classic of Schoolhouse Rock!, a series of musical cartoons about maths, science and grammar from the 1970s that can all be seen on the internet. My entry into the abacus world was only made possible by Kouzi Suzuki, a one-man soroban evangelist, who met me at a Tokyo rail station dressed up as Sherlock Holmes.

 

Andrews, F.E., New Numbers, Faber & Faber, London, 1936

Duodecimal Society of America, Inc., Manual of the Dozen System, Duodecimal Society of America, New York, 1960

Elbrow, Rear-Admiral G., The New English System of Money, Weights and Measures and of Arithmetic, P.S. King & Son, London, 1913

Essig, J., Douze, notre dix future, Dunod, Paris, 1955

Glaser, A., History of Binary and Other Nondecimal Numeration, Southampton, PA, 1971

Kawall Leal Ferreira, M. (ed.), Idéias Matemáticas de Povos Culturalmente Distintos, Global Editora, São Paulo, 2000

Suzuki, K., Lectures on Soroban, Institute for English Yomiagezan

 

Dowker, A., and Lloyd D., ‘Linguistic influences on numeracy’, Education Transactions, University of Bangor, 2005

Wassmann, J., and Dasen, P.R., ‘Yupno Number System and Counting’, Cross-cultural Psychology Journal, 1994

Hammarström, H., ‘Rarities in Numeral Systems’, 2007

CHAPTER TWO

Proofs Without Words is a gem, and was my source for the different Pythagoras proofs. Thanks to Tom Hull for much of the background about origami. The illustrations of how to make business-card tetrahedrons and cubes are inspired by his book. Another remarkable Japanese religio-geometric practice is sangaku, which didn’t fit in the chapter but is too fascinating not to mention here. A sangaku is a wooden tablet hung at a Buddhist or Shinto shrine that has a proof of a geometric prlem painted on it. Between the seventeenth and nineteenth centuries, thousands of sangaku were made by Japanese who had worked out geometrical problems but could not afford to publish them in books. Drawing the solutions on a tablet and hanging them at a shrine was a way of making a religious offering while also advertising their results.

Shortly before going to press, I learnt that Jerome Carter had died in a motorcycle accident in 2009.

 

Balliett, L.D., The Philosophy of Numbers, L.N. Fowler, 1908

Bell, E.T., Numerology, Century, 1933

Dudley, U., Numerology, Mathematical Association of America, 1997

du Sautoy, M., Finding Moonshine, Fourth Estate, London, 2008

Ferguson, K., The Music of Pythagoras, Walker, New York, 2008

Hull, T., Project Origami, A.K. Peters, Wellesley, MA, 2006

Kahn, C.H., Pythagoras and the Pythagoreans, a Brief History, Hackett, Indianapolis, IN, 2001

Loomis, E.S., The Pythagorean Proposition, Edwards Bros, Ann Arbor, MI, 1940

Maor, E., The Pythagorean Theorem, Princeton University Press, NJ, 2007

Mlodinow, L., Euclid’s Window, Free Press, New York, 2001

Nelsen, R.B., Proofs Without Words, Mathematical Association of America, Washington DC, 1993

Riedwig, C., Pythagoras, His Life, Teaching and Influence, Cornell University Press, Ithaca, NY, 2002

Schimmel, A., The Mystery of Numbers, Oxford University Press, New York, 1993

Simoons, F.J., Plants of Life, Plants of Death, University of Wisconsin Press, Madison, WI, 1998

Sundara Rao, T., Geometric Exercises in Paper Folding, Open Court, Chicago, IL, 1901

 

Bolton, N.J., and MacLeod, D.N.G., ‘The Geometry of the Sri Yantra’, Religion, vol. 7, 1977

Burnyeat, M.F., ‘Other Lives’, London Review of Books, 2007

CHAPTER THREE

Even though the Liber Abaci was first published in 1202, its first English translation did not appear until its 800th anniversary, in 2002. Vedic mathematics is not the only type of speed arithmetic in the market. There are several ‘systems’ and many of them share the same tricks. The best known is the Trachtenberg System, devised by Jakow Trachtenberg while a political prisoner in a Nazi concentration camp. Self-styled ‘mathemagician’ Arthur Benjamin is an entertaining, recent purveyor of the speed arithmetician’s art.

 

Fibonacci, L., Fibonacci’s Liber Abaci, Springer, New York, 2002

Joseph, G.G., Crest of the Peacock, Penguin, London, 1992

Knott, K., Hinduism: A Very Short Introduction, Oxford University Press, 1998

Seife, C., Zero, Souvenir Press, London, 2000

Tirthaji, Jagadguru Swami S. B. K., Vedic Mathematics, Motilal Banarsidass, Delhi, 1992

 

Dani, S.G., ‘Myths and reality: On “Vedic mathematics”’

CHAPTER FOUR

The least dweeby contestant in Leipzig was Rüdiger Gamm, a former bodybuilder who failed maths at school. After a career with exaggeratedly large biceps, he now has an exaggeratedly large brain. Gamm, whose calculation skills have made him a minor celebrity in Germany, told me that memory is his greatest asset: ‘I think I have [stored] 200,000 to 300,000 numbers in my head.’

(I found this chapter a challenge because of having to restrain myself from the temptation to make terrible puns about pi. Mathematicians have a congenital propensity to overpun. When we see a word we can’t help but break it down and rearrange it, which probably also explains why the world’s top Scrabble players are maths and computer-science graduates, not linguists.)

 

Arndt, J., and Haenel, C., Pi Unleashed, Springer, London, 2002

Beckmann, P., A History of Pi, St Martin’s Press, New York, 1971

Berggren L., Borwein J., and Borwein P., Pi: A Source Book, Springer, London, 2003

Bidder, G., A short Account of George Bidder, the celebrated Mental Calculator: with a Variety of the most difficult Questions, Proposed to him at the principal Towns in the Kingdom, and his surprising rapid Answers!, W.C. Pollard, 1821

Colburn, Z., A memoir of Zerah Colburn, written by himself, G. & C. Merriam, Springfield, MA, 1833

Rademacher, H., and Torplitz, O., The Enjoyment of Mathematics, Princeton University Press, NJ, 1957

 

Aitken, A.C., ‘The Art of Mental Calculation; with Demonstrations’, Society of Engineers Journal and Transactions, 1954

Preston, R., ‘The Mountains of Pi’, New Yorker, 1992

CHAPTER FIVE

Acheson, D., 1089 and all that, Oxford University Press, Oxford, 2002

Berlinski, D., Infinite Ascent, The Modern Library, New York, 2005

Dale, R., The Sinclair Story, Duckworth, London, 1985

Derbyshire, J., Unknown Quantity, Atlantic Books, London, 2006

Hopp, P.M., Slide Rules, Their History, Models and Makers, Astragal Press, New Jersey, 1999

Maor, E., e: The Story of a Number, Princeton University Press, NJ, 1994

Rade, L., and Kaufman, B.A., Adventures with Your Pocket Calculator, Pelican, London, 1980

Schlossberg, E., and Brockman, J., The Pocket Calculator Game Book, William Morrow, New York, 1975

Vine, J., Fun & Games with Your Electronic Calculator, Babani Press, London, 1977 (published in the US as Boggle, Price, Stern, Sloane Publishers, Los Angeles, CA, 1975)

CHAPTER SIX

The Mother Goose/Liber Abaci sequence of powers of seven also appears in modified form in Islamic folklore: the Angel of Mohammed is said to have 70,000 heads, each of which has 70,000 faces, each with 70,000 mouths, each with 70,000 tongues, each speaking 70,000 languages. Which makes a grand total of about 1.7 million billion billion languages.

I found Dudeney’s articles in Strand Magazine brilliantly well written, irrespective of the genius of the puzzles, and well worth a read. I am grateful to Angela Newing, the world expert on Henry Dudeney, for some of the biographical details, and to Jerry Slocum, for solving all my other puzzles about puzzles. If anyone wants an ambigram tattoo, check out Mark Palmer’s creations at www.wowtattoos.com.

 

Bachet, C.G., Amusing and Entertaining Problems that can be Had with Numbers (very useful for inquisitive people of all kinds who use arithmetic), Paris, 1612

Bodycombe, D.J., The Riddles of the Sphinx, Penguin, London, 2007

Danesi, M., The Puzzle Instinct, University of Indiana Press, Indianapolis, IN, 2002

Elffers, J., and Schuyt, M., Tangram, 1997

Gardner, M., Mathematics, Magic and Mystery, Dover, New York, 1956

Hardy, G.H., A Mathematician’s Apology, Cambridge University Press, Cambridge, 1940

Hooper, W., Rational Recreations, in which the principles of Numbers and Natural Philosophy are clearly and copiously elucidated by a series of easy, entertaining, interesting experiments, among which are all those commonly performed with the cards, London, 1774

Loyd, S., The 8th Book of Tan Part I, 1903; new edition Dover, New York, 1968

Maor, E., Trigonometric Delights, Princeton University Press, NJ, 1998

Netz, R., and Noel, W., The Archimedes Codex, Weidenfeld & Nicolson, London, 2007

Pasles, P.C., Benjamin Franklin’s Numbers, Princeton Universityess, NJ, 2008

Pickover, C.A., The Zen of Magic Squares, Circles and Stars, Princeton University Press, NJ, 2002

Rouse Ball, W.W., Mathematical Recreations and Problems, Macmillan, London, 1892

Slocum, J., The Tangram Book, Sterling, New York, 2001

Slocum, J., and Sonneveld, D., The 15 Puzzle, Slocum Puzzle Foundation, California, 2006

Swetz, F.J., Legacy of the Luoshu, Open Court, Chicago, IL, 2002

Dudeney, H., ‘Perplexities’, column in Strand Magazine, London, 1910–30

Singmaster, D., ‘The unreasonable utility of recreational mathematics’, lecture at the First European Congress of Mathematics, Paris, July 1992

CHAPTER SEVEN

The On-Line Encyclopedia of Integer Sequences (www.research.att.com/~njas/ sequences/) looks quite daunting at first to the non-specialist, but once you get the hang of it, is fascinating to surf. I found Chris Caldwell’s online encyclopedia of primes, The Prime Pages (www.primes.utm.edu) an excellent resource.

 

Doxiadis, A., Uncle Petros and Goldbach’s Conjecture, Faber & Faber, London, 2000

du Sautoy, M., The Music of the Primes, Fourth Estate, London, 2003

Reid, C., From Zero to Infinity, Thomas Y. Crowell, New York, 1955

 

Schmelzer, T., and Baillie, R., ‘Summing a curious, slowly convergent series’, American Mathematical Monthly, July 2008

Sloane, N.J.A., ‘My Favorite Integer Sequences’, 2000

CHAPTER EIGHT

It’s a curious quirk that pi, phi and Fibonacci sound related when their etymologies are all completely different, although conspiracy theorists might not be convinced. Separating the cranks from the non-cranks when it comes to the golden ratio is not always easy. One definite non-crank is Ron Knott, whose website: www.computing.surrey.ac.uk/personal/ext/ R.Knott/Fibonacci/ has all you ever wanted to know about 1.618…

 

Livio, M., The Golden Ratio, Review, London, 2002

Posamentier, A.S., and Lehmann, I., The (Fabulous) Fibonacci Numbers, Prometheus Books, New York, 2007

 

McManus, I.C., Cook, R., and Hunt, A., ‘Beyond the Golden Section and normative aesthetics: why do individuals differ so much in their aesthetic preferences for rectangles?’, Perception, vol. 36, 2007

CHAPTER NINE

The Kelly strategy is a lot more than just remembering the fraction 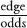, since gambling situations are usually more complex than the very simple one I described. I apologize to Ed Thorp, who asked hopefully during our interview if I would be able to spell out Kelly in proper detail. Sorry, Ed, it’s just too complicated for the scope of this book! William Poundstone’s terrific book was a guiding light and I’m grateful he supplied me with data for the graph chapter 9.

 

Aczel, A.D., Chance, High Stakes, London, 2005

Bennett, D.J., Randomness, Harvard University Press, Cambridge, MA, 1998

Devlin, K., The Unfinished Game, Basic Books, New York, 2008

Haigh, J., Taking Chances, Oxford University Press, Oxford, 1999

Kaplan, M., and Kaplan, E., Chances Are, Penguin, New York, 2006

Mlodinow, L., The Drunkard’s Walk, Allen Lane, London, 2008

Paulos, J.A., Innumeracy, Hill & Wang, New York, 1988

Poundstone, W., Fortune’s Formula, Hill & Wang, New York, 2005

Rosenthal, J.S., Struck by Lightning, Joseph Henry Press, Washington DC, 2001

Thorp, E.O., Beat the Dealer, Vintage, New York, 1966

Tijms, H., Understanding Probability, Cambridge University Press, 2007

Venn, J., The Logic of Chance, Macmillan, London, 1888

CHAPTER TEN

Statistics is the one field of maths covered in this book that I never studied at school or college, so much of this was very new to me. Some mathematicians don’t even consider statistics proper maths, occupied as it is with messy things like measurement. I enjoyed getting my hands dirty, although I’m not going back to Greggs for a very long time.

 

Blastland, M., and Dilnot, A., The Tiger That Isn’t, Profile, London, 2007

Brookes, M., Extreme Measures, Bloomsbury, London, 2004

Cline Cohen, P., A Calculating People: The Spread of Numeracy in Early America, University of Chicago Press, IL, 1982

Cohen, I. B., The Triumph of Numbers, W. W. Norton, New York, 2005

Edwards, A.W.F., Pascal’s Arithmetical Triangle, Johns Hopkins University Press, Baltimore, MD, 1987

Kuper S., and Szymanski S., Why England Lose, HarperCollins, London, 2009

Taleb, N.N., The Black Swan, Penguin, London, 2007

CHAPTER ELEVEN

While it is still an open question whether the universe is flat, spherical or hyperbolic, the universe is certainly pretty flat; if its curvature does indeed deviate from zero, it does so only very slightly. An irony of testing the universe for its curvature, however, is that it can never be conclusively proved that the universe is flat since there will always be measurement error. By contrast, it is theoretically possible to prove that the universe is curved, which would happen if the results produce a curvature, accounting for measurement error, that is non-zero.

The Hilbert Hotel sometimes goes by the name of Hotel Infinity, and the story has many different versions. The guests wearing T-shirts is my own adaptation.

 

Aczel, A.D., The Mystery of the Aleph, Washington Square Press, New York, 2000

Barrow, J.D., The Infinite Book, Jonathan Cape, London, 2005

Foster Wallace, D., Everything and More, W. W. Norton, New York, 2003

Kaplan, R., and Kaplan, E., The Art of the Infinite, Allen Lane, London, 2003

O’Shea, D., The Poincaré Conjecture, Walker, New York, 2007

 

Taimina, D., and Henderson, D.W., ‘How to Use History to Clarify Common Confusions in Geometry’, Mathematical Association of America Notes, 2005

INTERNET

It’s impossible to research anything to do with maths without referring to Wikipedia and Wolfram MathWorld (www.mathworld.wolfram.com), which I conferred with on a daily basis.

GENERAL

The number of books I looked through is too long to list all of them here, but these ones directly contributed in one way or another to the material in this book. Anything by Keith Devlin, Clifford A. Pickover or Ian Stewart is always worth a read.

 

Bell, E.T., Men of Mathematics, Victor Gollancz, London, 1937

Bentley, P.J., The Book of Numbers, Cassell Illustrated, London, 2008

Darling, D., The Universal Book of Mathematics, Wiley, Hoboken, NJ, 2004

Devlin, K., All the Math That’s Fit to Print, Mathematical Association of America, Washington DC, 1994

Dudley, U. (ed.), Is Mathematics Inevitable?, Mathematical Association of America, Washington DC, 2008

Eastaway, R., and Wyndham, J., Why Do Buses Come in Threes?, Robson Books, London, 1998

Eastaway, R., and Wyndham, J., How Long is a Piece of String?, Robson Books, London, 2002

Gowers, T., Mathematics: A Very Short Introduction, Oxford University Press, Oxford, 2002

Gullberg, J., Mathematics, W. W. Norton, New York, 1997

Hodges, A., One to Nine, Short Books, London, 2007

Hoffman, P., The Man Who Loved Only Numbers: The Story of Paul Erdös and the Search for Mathematical Truth, Fourth Estate, 1998

Hogben, L., Mathematics for the Million, Allen & Unwin, London, 1936

Mazur, J., Euclid in the Rainforest, Plume, New York, 2005

Newman, J. (ed.), The World of Mathematics, Dover, New York, 1956

Pickover, C.A., A Passion for Mathematics, Wiley, Hoboken, NJ, 2005

Singh, S., Fermat’s Last Theorem, Fourth Estate, London, 1997