Appendix Two

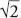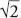In a unit square, the diagonal has length . To show that this is irrational I will use a proof by contradiction in which it is assumed that is rational, and then I will show how this leads to a contradiction. If it is contradictory to say that 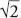is rational, it must be irrational.

If 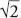is rational, then there are natural numbers a and b, such that 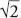= 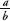. Let’s insist that this is the most reduced form of the fraction, so there is no way of rewriting 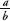as 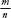when m and n are natural numbers less than a and b.

If 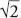= 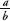, then by squaring both sides of the equation, 2 =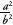 which we can rewrite as a²= 2b².

Whatever the value of b², 2b² must be even since multiplying any natural number by two makes an even number. If 2b² is even, then a2 is even. Now, since the square of an odd number is always an odd number, and the square of an even number is always even, this means that a must be even.

If a is even, then there is a number c less than a such that a = 2c, and therefore that a² = (2c)² = 4c².

By replacing a² with 4c² in the equation above, we get 4c² = 2b². Which reduces to b² = 2c². By the same reasoning, this means that b2 is even, so b is even. If b is even, there is a number d less than b such that b = 2dp>

Therefore 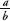can be rewritten 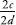, or 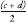since the 2s cancel. We have our contradiction! From above we have stipulated that 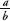is the most reduced form of the fraction, which means that there are no values for c and d less than a and b such that 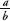= 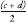. Since we have arrived at a contradiction by assuming that 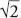can be written as 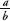it must be the case that 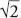cannot be written in such a way, so 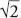is irrational.