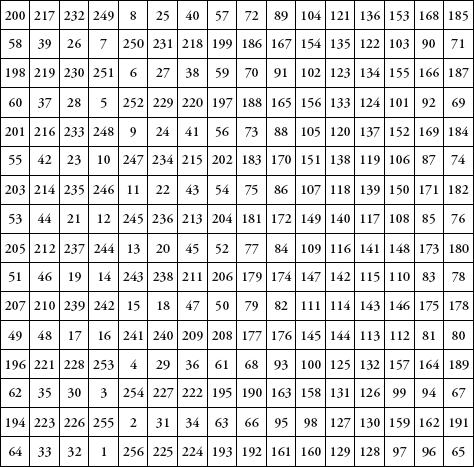
Appendix Three

In Franklin’s 16 × 16 magic square all the lines and columns add up to 2056. It is not a true magic square since the diagonals do not add up to 2056, but it is so rich in properties that Clifford A. Pickover writes that ‘it is no exaggeration to say that one could spend a lifetime contemplating its wonderful structure’. For example, every 2 × 2 subsquare (and there are 225 of those) adds up to 514, which means that every 4 × 4 subsquare adds up to 2056. Many other symmetries and patterns are also contained in the square.